决策树生成算法
决策树是机器学习领域非常重要的一种方法,是一种树结构(二叉树或多叉树),树的每个非叶子结点表示在一个属性上的测试,每个分支表示属性在某个值域上的输出,叶子结点代表类别,由所有落在该叶子结点上的所有样本决定。看个简单的例子
| # | Weather | Temperature | Air Quality | Running |
|---|---|---|---|---|
| 1 | sunny | hot | excellent | No |
| 2 | sunny | cool | excellent | Yes |
| 3 | sunny | cool | good | Yes |
| 4 | sunny | cool | polluted | No |
| 5 | rainy | cool | excellent | No |
| 6 | rainy | hot | excellent | No |
假设我们有一些数据,我们会根据当天的天气、气温、空气状况来决定是否去公园跑步。使用这些数据,我们可以构建下面这样一棵决策树
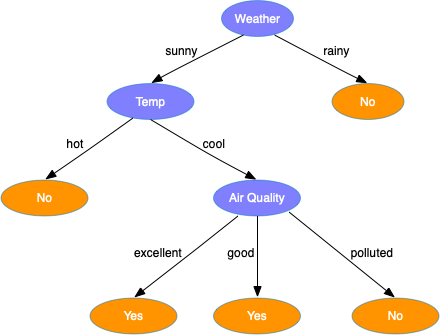
决策树是如何生成的,每个结点应该选择哪个属性分裂?下面将介绍常见的生成决策树的几种方法。
ID3
熵
熵(Entropy)是热力学中表征物质状态的参量之一,用来度量一个系统的混乱程度。系统越混乱熵越大,反之熵越小。1948年,克劳德·艾尔伍德·香农将热力学熵的概念引入到信息论中,用来度量不确定度,故又称信息熵或香农熵。一个离散型随机变量 $X$ 的熵 $H(X)$ 定义为
\[H(X) = -\sum_{x \in X} p(x)\log p(x)\]熵越大,不确定性越高,包含的信息量越大;熵越小,不确定性越低,包含的信息量越少。
信息增益
一个样本集合 $S$ 按属性 $A$ 的值划分为多个子集,则属性 $A$ 对数据集 $S$ 划分的期望信息为
\[Info_A(S) = \sum_{v \in A} \frac{\vert S_v \vert}{\vert S \vert}H(S_v)\]其中,$S_v$ 为样本集合中所有属性 $A$ 值为 $v$ 的样本集合,$\vert S_v \vert$ 表示集合 $S_v$ 中样本的数量。通过属性 $A$ 对数据集 $S$ 划分后熵减少的度称为信息增益(Information Gain)
\[InfoGain(S,A) = H(S) - Info_A(S)\]信息增益表示得知属性 $A$ 的信息后样本集合不确定度减少的程度。
ID3算法在构建决策树的过程中,每次选择使得样本划分后信息增益最大的属性进行分裂,这就是ID3算法的核心思想。
以本文开头的样本数据为例,我们看一下如何使用ID3算法生成一棵决策树:
-
我们首先计算使用各个属性对数据集划分的期望信息
\[Info_{Weather} = {2 \over 3} \times (-{1 \over 2}\log {1 \over 2} - {1 \over 2}\log {1 \over 2}) + {1 \over 3} \times (-1\log1) = 0.6667 \\ Info_{Temperature} = {2 \over 3} \times (-{1 \over 2}\log {1 \over 2} - {1 \over 2}\log {1 \over 2}) + {1 \over 3} \times (-1\log1) = 0.6667 \\ Info_{Air Quality} = {2 \over 3} \times (-{1 \over 4}\log {1 \over 4} - {3 \over 4} \log {3 \over 4}) + {1 \over 6} \times (-1 \log 1) + {1 \over 6} \times (-1 \log 1) = 0.5409\]可以看到使用空气质量划分可以获得最大的信息增益,于是使用空气质量进行分裂得到
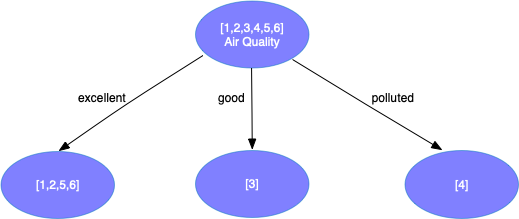
-
对第2层第1个结点分裂,计算使用属性Weather和Temperature划分的期望信息
\[Info_{Weather} = {1 \over 2} \times ({-{1 \over 2}\log{1 \over 2} - {1 \over 2}\log{1 \over 2}}) + {1 \over 2} \times (-1 \log 1) = 0.5 \\ Info_{Temperature} = {1 \over 2} \times ({-{1 \over 2}\log{1 \over 2} - {1 \over 2}\log{1 \over 2}}) + {1 \over 2} \times (-1 \log 1) = 0.5\]使用天气和温度划分可以得到一样的信息增益,随机选择天气进行分裂得到
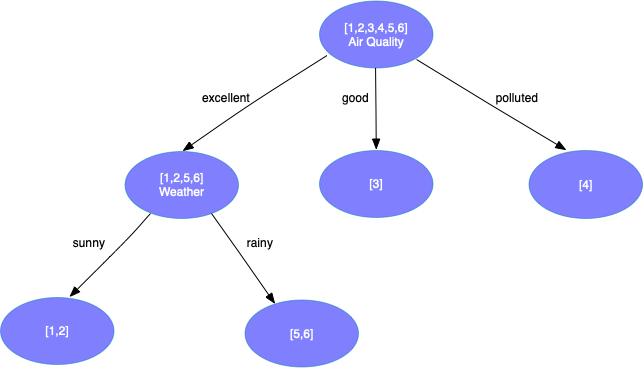
- 对第2层第2个结点分裂,我们发现该结点只包含一个样本,于是将其标记为叶子结点,其类别为样本3的类别;同理可以处理第2层第3个结点。
-
对第3层第1个结点分裂,这时只剩一个属性Temperature,直接使用该属性分裂得到
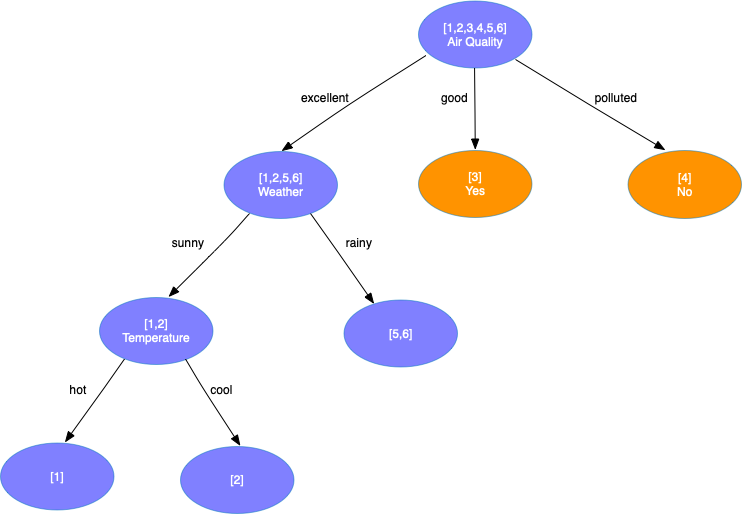
- 对第3层第2个结点分裂,我们发现该结点上所有样本的类别一致,因此停止分裂并将其标记为叶子结点,其类别为该结点上所有样本类别中最多的一个(这里只有1个)。
-
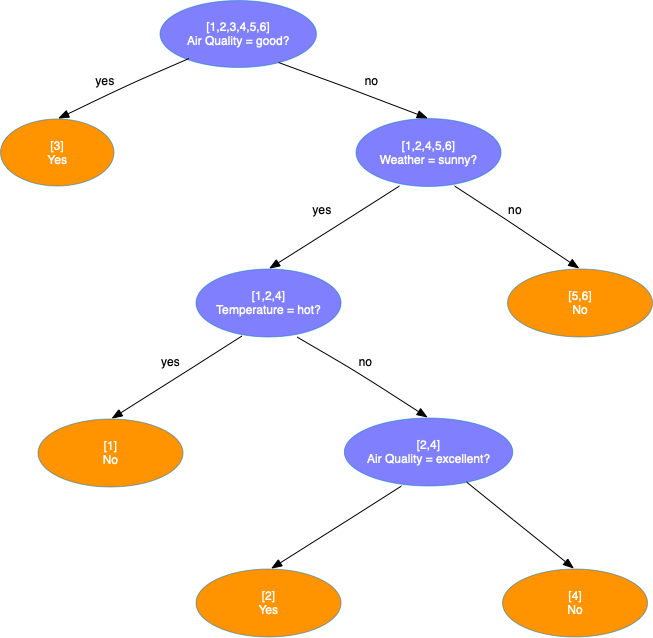
处理第4层结点,发现第4层所有结点都只有1个样本,于是将其标记为叶子结点并停止。最终生成的决策树如下
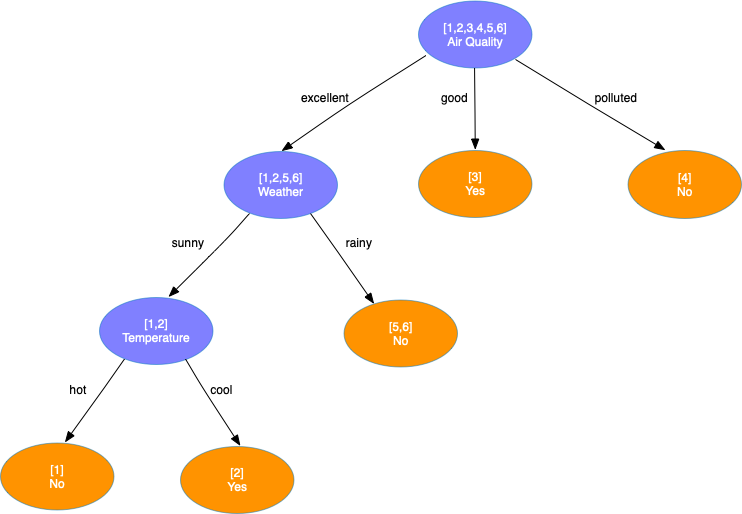
ID3算法存在两个明显的缺点:
- ID3算法使用信息增益做为选择分支属性的依据,而信息增益倾向于选择值类别较多的属性,在有些情况下这类属性可能不会提供太多有用信息。
- ID3算法只能对属性值为离散值的数据集构造决策树。
C4.5
信息增益率
定义样本集合 $S$ 在属性 $A$ 的分裂信息(Split Information)为
\[SplitInfo_A(S) = -\sum_{v \in A} \frac{\vert S_v \vert}{\vert S \vert} \log \frac{\vert S_v \vert}{\vert S \vert}\]则通过属性 $A$ 分裂之后的信息增益率为
\[InfoGainRatio_A(S) = \frac{InfoGain(S,A)}{SplitInfo_A(S)}\]C4.5算法通过信息增益率选择分裂属性,克服了ID3算法倾向于选择值类别较多的属性这个缺点。
连续属性处理
与ID3算法只能处理离散属性不同,C4.5增加了支持处理连续属性。假设属性 $A$ 是连续属性,其值按从小到大排列为 $\lbrace x_1, x_2, …, x_n \rbrace$, 通过二分法将属性 $A$ 的值划分为两部分,共有 $n-1$ 种划分方法。对于第i种划分,取 $\theta_i = \frac{x_i + x_{i+1}}{2}$, 将属性 $A$ 上值不大于 $\theta_i$ 的样本划分到一个集合,大于 $\theta_i$ 的样本划分到另一个集合,然后计算此种划分方法下的信息增益率,并选择信息增益率最大的划分方法。
还是以上面的数据为例,看一下使用C4.5算法生成决策树的过程:
-
计算各个属性的分裂信息
\[SplitInfo_{Weather} = -{2 \over 3}\log{2 \over 3} - {1 \over 3}\log{1 \over 3} = 0.9183 \\ SplitInfo_{Temperature} = -{2 \over 3}\log{2 \over 3} - {1 \over 3}\log{1 \over 3} = 0.9183 \\ SplitInfo_{Air Quality} = -{2 \over 3}\log{2 \over 3} - {1 \over 6}\log{1 \over 6} - {1 \over 6}\log{1 \over 6} = 1.2516\]对应的信息增益率为
\[InfoGainRatio_{Weather} = \frac{0.9183-0.6667}{0.9183} = 0.27398 \\ InfoGainRatio_{Temperature} = \frac{0.9183-0.6667}{0.9183} = 0.27398 \\ InfoGainRatio_{Air Quality} = \frac{0.9183-0.5409}{1.2516} = 0.30153\]于是使用属性空气质量进行分裂得到

-
对第2层第1个结点分裂,计算使用属性Weather和Temperature划分的分裂信息
\[SplitInfo_{Weather} = -{1 \over 2}\log{1 \over 2} - {1 \over 2}\log{1 \over 2} = 1 \\ SplitInfo_{Temperature} = -{1 \over 2}\log{1 \over 2} - {1 \over 2}\log{1 \over 2} = 1\]对应的信息增益率为
\[InfoGainRatio_{Weather} = \frac{0.9183-0.5}{1} = 0.4183 \\ InfoGainRatio_{Temperature} = \frac{0.9183-0.5}{1} = 0.4183\]二者信息增益率一样,因此可以随机选择一个进行分裂。和ID3过程类似,最终我们可以得到如下决策树

CART
Gini系数
对样本集合 $S$, 定义其Gini系数为
\[Gini(S) = \sum_i p_i(1-p_i) = 1 - \sum_i p_i^2\]其中,$p_i$ 表示样本集合中类别为 $C_i$ 的样本的所占的比例。Gini系数的计算要比熵模型简单很多,可以作为熵模型的近似替代。
若属性 $A$ 将集合 $S$ 划分为两个集合 $S_1$ 和 $S_2$, 划分后的Gini增益
其中
\[Gini_A(S) = \frac{\vert S_1 \vert}{\vert S \vert} Gini(S_1) + \frac{\vert S_2 \vert}{\vert S \vert} Gini(S_2)\]CART(Classfication And Regression Tree)使用Gini增益来选择分裂属性,与ID3和C4.5会生成多个分支不同,CART算法只对属性进行二分,因此CART算法生成的是二叉树而不是多叉树。
同样以上面的数据为例,我们看一下CART算法生成决策树的过程:
-
计算以各属性类别二分样本的Gini系数
\[Gini_{sunny} = {2 \over 3} \times (1 - ({1 \over 2})^2 - ({1 \over 2})^2) + {1 \over 3} \times (1 - 1^2) = 0.3333 \\ Gini_{hot} = {2 \over 3} \times (1 - ({1 \over 2})^2 - ({1 \over 2})^2) + {1 \over 3} \times (1 - 1^2) = 0.3333 \\ Gini_{excellent} = {2 \over 3} \times (1 - ({1 \over 4})^2 - ({3 \over 4})^2) + {1 \over 3} \times (1 - ({1 \over 2})^2 - ({1 \over 2})^2) = 0.4167 \\ Gini_{good} = {1 \over 6} \times (1 - 1^2) + {5 \over 6} \times (1 - ({1 \over 5})^2 - ({4 \over 5})^2) = 0.2667 \\ Gini_{poluted} = {1 \over 6} \times (1 - 1^2) + {5 \over 6} \times (1 - ({2 \over 5})^2 - ({3 \over 5})^2) = 0.4000 \\\]选择天气属性为 good 划分样本可以获得最大的Gini增益
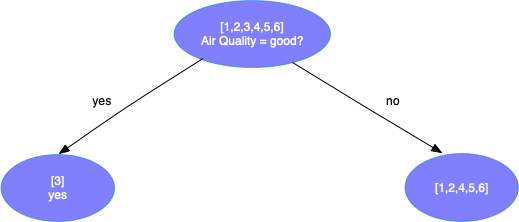
-
对第2层第1个结点分裂,由于其只包含一个样本,将其标记为叶子结点,类别为该样本类别。接着分裂第2个结点,计算Gini系数
\[Gini_{sunny} = {3 \over 5} \times (1 - ({1 \over 3})^2 - ({2 \over 3})^2) + {2 \over 5} \times (1 - 1^2) = 0.2667 \\ Gini_{hot} = {2 \over 5} \times (1 - 1^2) + {3 \over 5} \times (1 - ({1 \over 3})^2 - ({2 \over 3})^2) = 0.2667 \\ Gini_{excellent} = {4 \over 5} \times (1 - ({1 \over 4})^2 - ({3 \over 4})^2) + {1 \over 5} \times (1 - 1^2) = 0.3000 \\\]在天气为sunny和温度为hot的属性值上分裂,可以获得最大的增益。选择天气为sunny的属性进行分裂
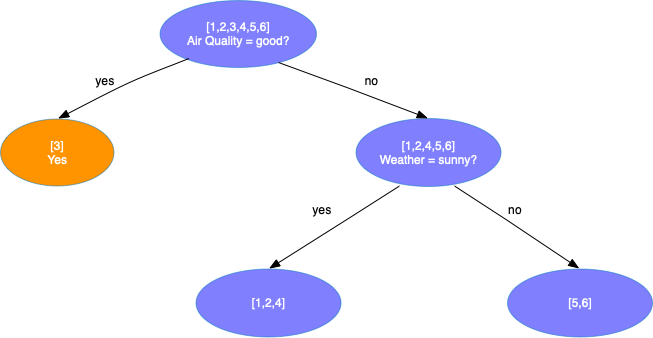
-
接着分裂第3层第1个结点
\[Gini_{hot} = {1 \over 3} \times (1 - 1^2) + {2 \over 3} \times (1 - ({1 \over 2})^2 - ({1 \over 2})^2) = 0.3333 \\ Gini_{excellent} = {1 \over 3} \times (1 - 1^2) + {2 \over 3} \times (1 - ({1 \over 2})^2 - ({1 \over 2})^2) = 0.3333 \\\]选择温度为hot的属性进行分裂。然后对剩余的结点做同样的处理,最终得到决策树