中心性算法

中心性算法（Centrality Algorithms）用于识别图中特定节点的角色及其对网络的影响。中心性算法能够帮助我们识别最重要的节点，帮助我们了解组动态，例如可信度、可访问性、事物传播的速度以及组与组之间的连接。尽管这些算法中有许多是为社会网络分析而发明的，但它们已经在许多行业和领域中得到了应用。

下图罗列了我们所有需要了解的中心性算法指标:

Degree Centrality

Degree Centrality (度中心性)是一种以度作为标准的中心性指标。

Degree 统计了一个节点直接相连的边的数量，包括出度和入度。Degree 可以简单理解为一个节点的访问机会的大小。例如，在一个社交网络中，一个拥有更多 degree 的人（节点）更容易与人发生直接接触，也更容易获得流感。

一个网络的平均度 (average degree)，是边的数量除以节点的数量。当然，平均度很容易被一些具有极大度的节点 “带跑偏” （skewed）。所以，度的分布（degree distribution）可能是表征网络特征的更好指标。

如果你希望通过出度入度来评价节点的中心性，就可以使用 degree centrality。度中心性在关注直接连通时具有很好的效果。

Closeness Centrality

Closeness Centrality (紧密性中心性)是一种检测能够通过子图有效传播信息的节点的方法。紧密性中心性计量一个节点到所有其他节点的紧密性（距离的倒数），一个拥有高紧密性中心性的节点拥有着到所有其他节点的距离最小值。

对于一个节点来说，紧密性中心性是节点到所有其他节点的最小距离和的倒数：

\[C(u) = \frac{1}{\sum_{v \neq u} d(u, v)}\]

其中$u$是我们要计算紧密性中心性的节点，$d(u,v)$代表节点$u$与节点$v$的最短路径距离。更常用的公式是归一化之后的中心性，即计算节点到其他节点的平均距离的倒数

\[C(u) = \frac{n-1}{\sum_{v \neq u} d(u, v)}\]

其中，$n$为图中顶点数。

如果图是一个非连通图，那么我们将无法通过上面的公式计算紧密性中心性。那么针对非连通图，可以使用调和中心性（Harmonic Centrality)

\[H(u) = \sum_{v \neq u} \frac{1}{d(u,v)}\]

归一化版本为

\[H(u) = \frac{1}{n-1} \sum_{v \neq u} \frac{1}{d(u,v)}\]

Wasserman and Faust 提出过另一种计算紧密性中心性的公式，专门用于包含多个子图并且子图间不相连接的非连通图：

\[WF(u) = \frac{n-1}{N-1} (\frac{n-1}{\sum_{v \neq u} d(u, v)})\]

其中，$N$是图中总的节点数量，$n$是一个部件（component）中的节点数量。

当我们希望关注网络中传播信息最快的节点，我们就可以使用紧密性中心性。

Betweenness Centrality

中介中心性（Betweenness Centrality）是一种检测节点对图中信息或资源流的影响程度的方法。它通常用于寻找连接图的两个部分的桥梁节点。

中介中心性算法首先计算连接图中每对节点之间的最短（最小权重和）路径。每个节点都会根据这些通过节点的最短路径的数量得到一个分数。节点所在的路径越短，其得分越高。

\[B(u) = \sum_{s \neq u \neq t} \frac{|P(u)|}{|P|}\]

$P$表示从顶点s到t的所有最短路径，$P(u)$表示从$s$到$t$的所有最短路径中经过$u$的路径，$

P

$表示路径的数量。在一张大图上计算中介中心性的代价是十分昂贵的，通常会使用一些成本更小，速度更快，精度大致相当的近似算法来代替。

PageRank

PageRank 是所有中心性算法中最著名的一个，以谷歌联合创始人拉里·佩奇的名字命名，它测量节点传递影响的能力。PageRank基于下面两个假设：

1. 数量假设：在Web图模型中，如果一个页面节点接收到的其他网页指向的入链数量越多，那么这个页面越重要。
2. 质量假设：指向页面A的入链质量不同，质量高的页面会通过链接向其他页面传递更多的权重。所以越是质量高的页面指向页面A，则页面A越重要。

\[PR(u) = (1 - d) + d(\sum_{v \to u} \frac{PR(v)}{C(v)})\]

$d$ 是阻尼系数(damping factor)，表示一个用户继续向后浏览的概率，一般取0.85。$v$ 是所有指向$u$的顶点，$C(v)$ 是顶点$v$的出链数。

社群发现算法

识别社群对于评估群体行为或突发事件至关重要。对于一个社群来说，内部节点与内部节点的关系（边）比社群外部节点的关系更多。识别这些社群可以揭示节点的分群，找到孤立的社群，发现整体网络结构关系。社群发现算法（Community Detection Algorithms）有助于发现社群中群体行为或者偏好，寻找嵌套关系，或者成为其他分析的前序步骤。社群发现算法也常用于网络可视化。

下图是社群发现算法的分类:

Measuring Algorithm

三角计数（Triangle Count）和聚类系数（Clustering Coefficient）经常被一起使用。三角计数计算图中由节点组成的三角形的数量，要求任意两个节点间有边（关系）连接。聚类系数算法的目标是测量一个组的聚类紧密程度。该算法计算网络中三角形的数量，与可能的关系的比率。聚类系数为 1 表示这个组内任意两个节点之间有边相连。

有两种聚类系数：局部聚类系数（Local Clustering Coefficient）和全局聚类系数（Global Clustering Coefficient）。

局部聚类系数计算一个节点的邻居之间的紧密程度，计算时需要三角计数。计算公式：

\[CC(u) = \frac{2R_u}{k_u (k_{u} - 1)}\]

$R(u)$ 代表经过节点 $u$ 和它的邻居的三角形个数，$k(u)$ 代表节点 $u$ 的度。

全局聚类系数是局部聚类系数的归一化求和。

Components Algorithm

强关联部件（Strongly Connected Components，简称 SCC）算法寻找有向图内的一组一组节点，每组节点可以通过关系互相访问。在 “Community Detection Algorithms” 的图中，我们可以发现，每组节点内部不需要直接相连，只要通过路径访问即可。

关联部件（Connected Components）算法，不同于 SCC，组内的节点对只需通过一个方向访问即可。

关联类算法作为图分析的早期算法，用以了解图的结构，或确定可能需要独立调查的紧密集群十分有效。对于推荐引擎等应用程序，也可以用来描述组中的类似行为等等。许多时候，算法被用于查找集群并将其折叠成单个节点，以便进一步进行集群间分析。对于我们来说，先运行以下关联类算法查看图是否连通，是一个很好的习惯。

Label Propagation Algorithm

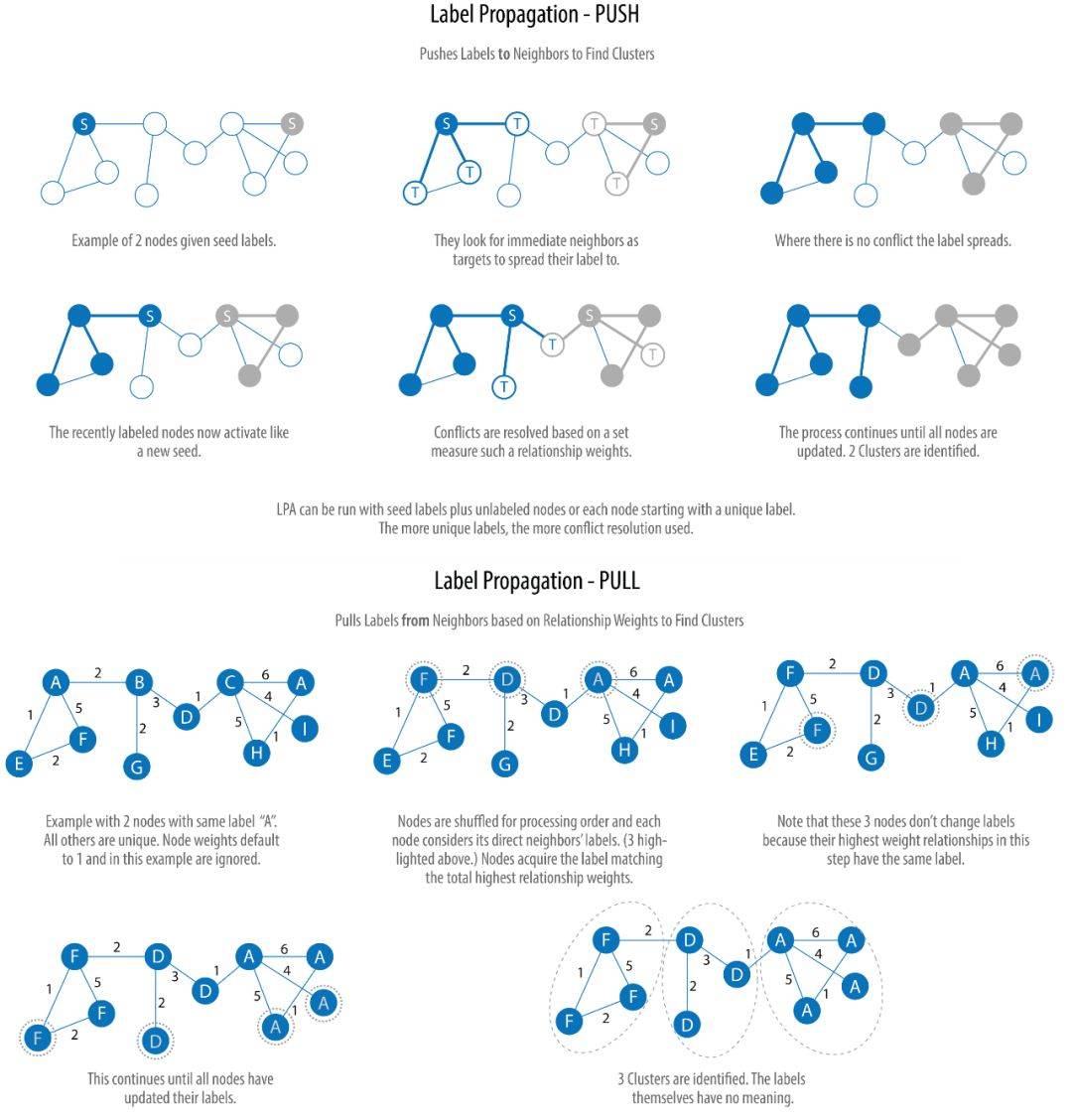
标签传播算法（Label Propagation Algorithm，简称 LPA）是一个在图中快速发现社群的算法。在 LPA 算法中，节点的标签完全由它的直接邻居决定。算法非常适合于半监督学习，你可以使用已有标签的节点来种子化传播进程。

LPA 是一个较新的算法，由 Raghavan 等人于 2007 年提出。我们可以很形象地理解算法的传播过程，当标签在紧密联系的区域，传播非常快，但到了稀疏连接的区域，传播速度就会下降。当出现一个节点属于多个社群时，算法会使用该节点邻居的标签与权重，决定最终的标签。传播结束后，拥有同样标签的节点被视为在同一群组中。

下图展示了算法的两个变种：Push 和 Pull。其中 Pull 算法更为典型，并且可以很好地并行计算：

Louvain Modularity Algorithm

Louvain算法是基于模块度的社区发现算法，该算法在效率和效果上都表现较好，并且能够发现层次性的社区结构，其优化目标是最大化整个社区网络的模块度。

模块度（Modularity）是评估一个社区网络划分好坏的度量方法，它的物理含义是社区内节点的连边数与随机情况下的边数只差，它的取值范围是 [−1/2,1)，其定义如下：

\(Q = \frac{1}{2m} \sum_{i,j}[A_{i,j} - \frac{k_i k_j}{2m}] \delta(c_i, c_j)\) \(\delta(u, v) = \begin{cases} 1 & \text{u == v} \\ 0 & \text{else} \end{cases}\)

其中，$A_{i,j}$ 表示顶点 $i$ 和 $j$ 之间边的权重，在无权网络中可以看作是1； $k_i = \sum_{j}A_{i,j}$ 表示所有与顶点 $i$ 相连的边的权重之和；$c_i$ 表示节点 $i$ 所属的社区；$m=\frac{1}{2}\sum_{i,j}A_{i,j}$ 表示所有边的权重之和。节点 $j$ 连接到任意一个结点的概率是 $\frac{k_j}{2m}$, 现在节点 $i$ 有 $k_i$ 的度，因此在随机情况下节点 $j$ 与 $i$ 连接的边为 $k_i \frac{k_j}{2m}$。

模块度的公式可作如下简化:

\[\begin{align} Q & = \frac{1}{2m} \sum_{i,j}[A_{i,j} - \frac{k_i k_j}{2m}] \delta(c_i, c_j) \\ & = \frac{1}{2m} [\sum_{i,j}A_{i,j} - \frac{\sum_{i}k_i \sum_{j} k_j}{2m}]\delta(c_i, c_j) \\ & = \frac{1}{2m} \sum_{c} [\sum_{in} - \frac{(\sum_{tot})^2}{2m}] \\ & = \sum_{c} [\frac{\sum_{in}}{2m} - (\frac{\sum_{tot}}{2m})^2] \\ & = \sum_{c} [e_c - a_c^2] \end{align}\]

其中，$\sum_{in}$ 表示社区 $c$ 内的的边的权重之和，$\sum_{tot}$ 表示与社区 $c$ 内的节点相连的的边的权重之和。这样模块度也可以理解是社区内部边的权重减去所有与社区节点相连的边的权重和，对无向图更好理解，即社区内部边的度数减去社区内节点的总度数。

基于模块度的社区发现算法，都是以最大化模块度Q为目标。

Louvain算法的思想很简单：

1. 将图中的每个节点看成一个独立的社区，初始社区的数目与节点个数相同；

2. 对每个节点i，依次尝试把节点i分配到其每个邻居节点所在的社区，计算分配前与分配后的模块度变化Δ𝑄，并记录Δ𝑄最大的那个邻居节点，如果𝑚𝑎𝑥Δ𝑄>0，则把节点i分配Δ𝑄最大的那个邻居节点所在的社区，否则保持不变；

3. 重复2），直到所有节点的所属社区不再变化；

4. 对图进行压缩，将所有在同一个社区的节点压缩成一个新节点，社区内节点之间的边的权重转化为新节点的环的权重，社区间的边权重转化为新节点间的边权重；

5. 重复1）直到整个图的模块度不再发生变化。

从流程来看，该算法能够产生层次性的社区结构，其中计算耗时较多的是最底一层的社区划分，节点按社区压缩后，将大大缩小边和节点数目，并且计算节点 $i$ 分配到其邻居 $j$ 时模块度的变化只与节点 $i、j$ 的社区有关，与其他社区无关，因此计算很快。在论文中，把节点 $i$ 分配到邻居节点 $j$ 所在的社区 $c$ 时模块度变化为：

\[\Delta Q = [\frac{\sum_{in} + k_{i,in}}{2m} - (\frac{\sum_{tot} + k_i}{2m})^2] - [\frac{\sum_{in}}{2m} - (\frac{\sum_{tot}}{2m})^2 - (\frac{k_i}{2m})^2]\]

其中 $k_{i,in}$ 是社区 $c$ 内节点与节点i的边权重之和，注意对 $k_{i,in}$ 是对应边权重加起来再乘以2，这点在实现时很容易犯错。

$\Delta Q$ 分了两部分，前面部分表示把节点 $i$ 加入到社区 $c$ 后的模块度，后一部分是节点i作为一个独立社区和社区 $c$ 的模块度。在实现的时候模块度变化还可以简化，把上面的公式展开，很多项就抵消了，化简之后：

\[\Delta Q = [\frac{k_{i,in}}{2m} - \frac{\sum_{tot} k_i}{2m^2}]\]

论文中指出，算法第2）步节点的顺序会对分群结果又一定影响，但分群效果差距不大，只是会影响算法的时间效率，还有论文指出按度数从大的小的顺序处理速度最快。

下图给出了一个粗略的步骤，帮助我们理解算法如何能够多尺度地构建社群：

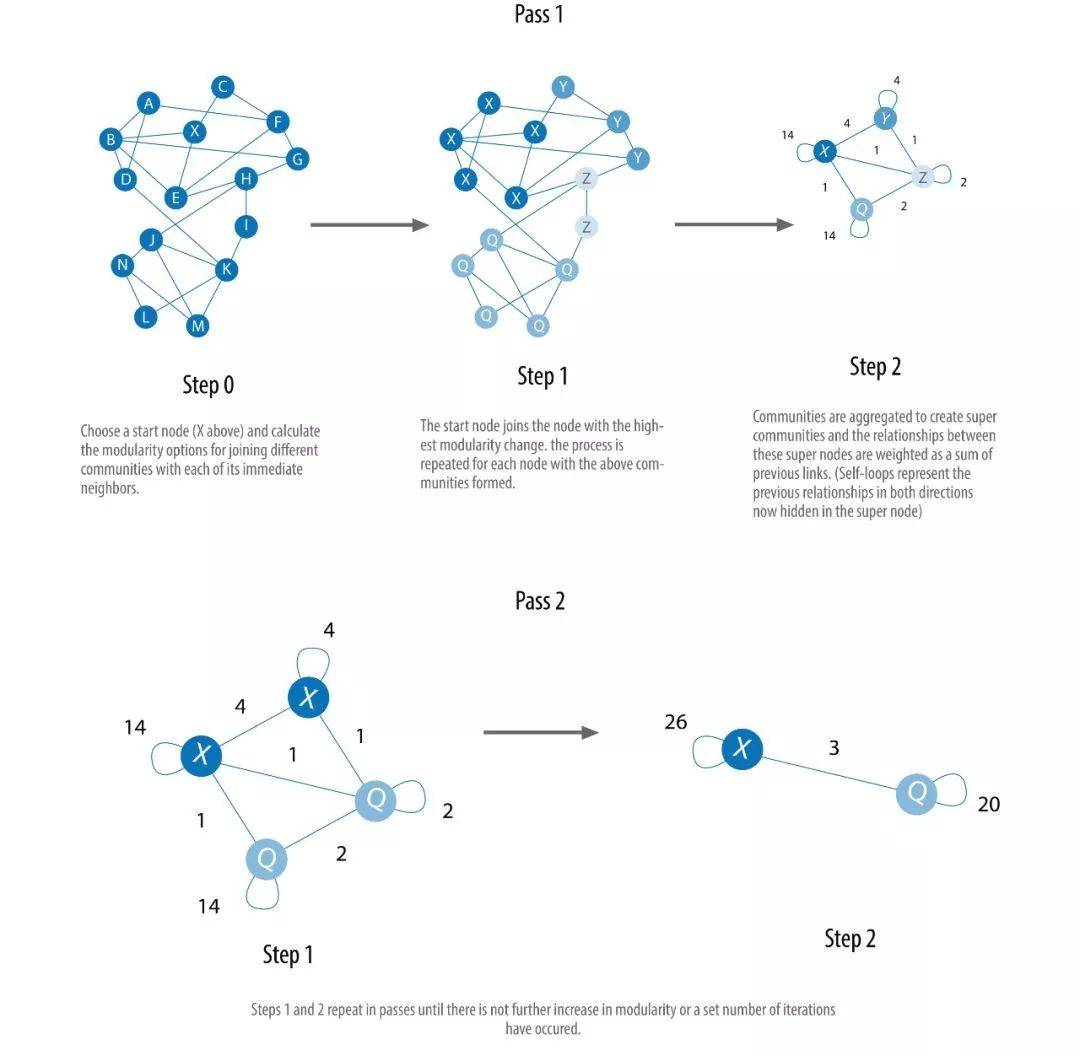
Louvain Modularity 算法非常适合庞大网络的社群发现，算法采用启发式方式从而能够克服传统 Modularity 类算法的局限。算法应用：

检测网络攻击:该算可以应用于大规模网络安全领域中的快速社群发现。一旦这些社群被发现，就可以用来预防网络攻击；

主题建模：从 Twitter 和 YouTube 等在线社交平台中提取主题，基于文档中共同出现的术语，作为主题建模过程的一部分。