大多数机器学习的问题，最终都是求解一个目标函数 $J(\theta)$ 的极值，即最优化问题。优化方法在机器学习算法的推导与实现中占据重要的地位，本文主要介绍一些常用的优化方法，理解它们的原理及实现方法。

梯度下降

梯度下降(Gradient Descent)是机器学习领域最流行的优化方法之一，它的核心思想是，在任意一点，函数值在负梯度的方向是下降最快的，因此沿着负梯度的方向搜索，逐步逼近最小值。梯度下降的参数更新公式如下

\[\theta_{t+1} = \theta_t - \eta \nabla_{\theta}J(\theta)\]

其中，$\eta$ 是学习速率，决定了每一步学习的步长。
梯度下降有三个变种，分别是批梯度下降(Batch Gradient Descent, BGD)、随机梯度下降(Stochastic Gradient Descent, SGD)和小批量梯度下降(Mini-Batch Gradient Descent, MBGD)。这三个变种的主要区别是，BGD每次更新参数时使用所有的样本来计算 $J(\theta)$，而SGD每次只使用一个样本，MBGD每次使用m个样本。

SGD-M

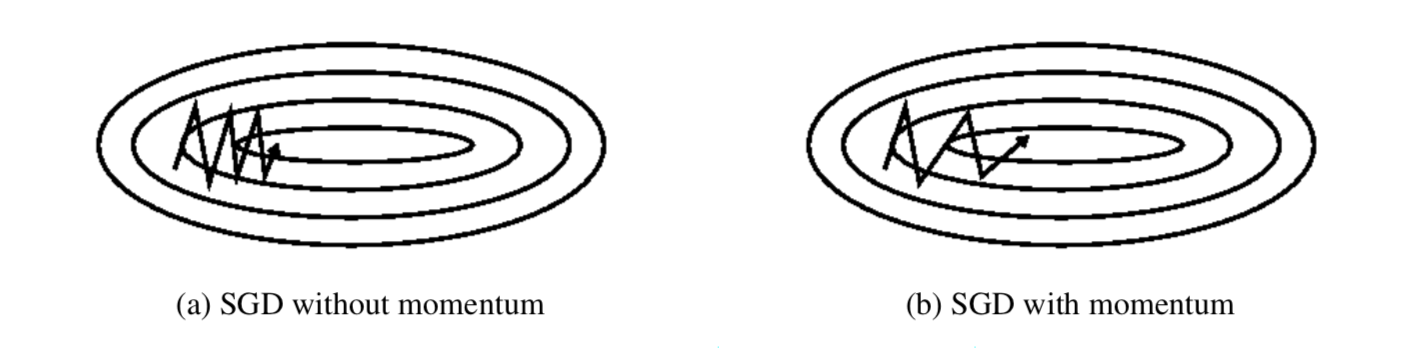
SGD收敛速度慢，在遇到沟壑时容易陷入震荡。SGD-M在SGD的基础上引入了动量项(Momentum)来加快梯度下降的速度，并减少震荡。动量项累积了之前迭代时的梯度值

\[v_{t+1} = \gamma v_{t} + \eta \nabla_{\theta} J(\theta)\] \[\theta_{t+1} = \theta_{t} - v_{t+1}\]

$\gamma$ 是动量项系数，一般取0.9左右。这样参数的更新方向就不仅仅由当前梯度方向决定，也与此前累积的梯度方向有关。如果梯度方向变化不大可以加速更新，梯度方向变化较大可以减少更新幅度。由此产生加速更新和减小震荡的效果。

Nesterov Accelerated Gradient

我们并不满足于算法沿着梯度下降的方向更新参数 $\theta$, 而是希望当参数快要到达极小值的时候能减小更新速率，NAG通过一种“预知未来”的方式实现了这一点。与SGD-M通过 $t$ 时刻 $\theta$ 位置处的梯度更新参数不同，NAG会根据 $t+1$ 时刻 $\theta$ 处的梯度来更新参数，因而可以在目标函数有增高趋势前降低更新速率。在SGD-M中，我们使用下式更新参数

\[\begin{aligned} \theta_{t+1} & = \theta_{t} - v_{t+1} \\ & = \theta_t - (\gamma v_t + \nabla_{\theta} J(\theta)) \end{aligned}\]

在更新 $\theta$ 前，我们没有办法准确地知道 $t+1$ 时刻 $\theta$ 的位置，但是我们可以使用 $\theta_t - \gamma v_t$ 来近似，因此NAG更新参数的公式为

\[v_{t+1} = \gamma v_{t} + \eta \nabla_{\theta} J(\theta - \gamma v_{t})\] \[\theta_{t+1} = \theta_t - v_{t+1}\]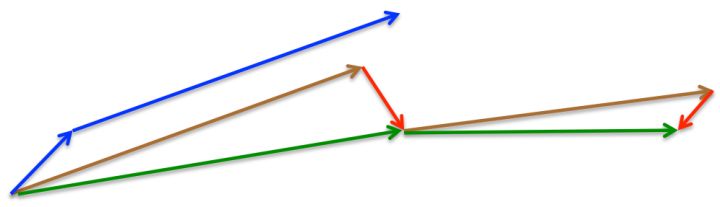

上图中蓝线是SGD-M更新参数的方式，它会先计算梯度(短蓝线)，然后加上累积梯度(长蓝线)；而NAG会先沿累积梯度方向移动(棕线)，然后计算该处的梯度(红线)，再做一个校正(绿线)，这样就得到最终更新后的参数值。

Adagrad

GD, SGD-M, NAG均以相同的学习速率去更新 $\theta$ 的各个分量，而深度学习往往涉及大量的参数，不同参数的更新频率也有所不同。对于更新频繁的参数，我们希望学习速率小一些，以使学到的参数更稳定；而对于更新不频繁的参数，我们希望学习速率大一些，每次多学习一些知识，Adagrad算法可以做到这一点。

\[\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{G_t + \epsilon}} g_t\] \[G_t = \sum_{i=1}^{t} g_i^2\] \[g_t = \nabla_{\theta_t} J(\theta_t)\]

$G_t$ 表示从初始时刻到时刻t梯度的平方和；$\epsilon$ 是平滑项，主要是为了防止除0，一般取 $1e-8$；$\eta$ 一般取0.01。 可以这样理解，对于频繁更新的项，$G_t$ 会越来越大，学习速率也就越来越小。Adagrad在稀疏数据上表现良好。

Adadelta

在Adagrad算法中，$G_t$ 是单调递增的，因而导致学习速率越来越小。为了改善这个问题，Adadelta会限制计算 $G_t$ 的窗口大小，即只计算过去 $w$ 个时刻梯度的平方和。当然，为每个分量存储 $w$ 个梯度是低效的，Adadelta使用指数衰减均值

\[E_{t+1} = \gamma E_t + (1 - \gamma) g_t^2\]

用 $\Delta \theta_t$ 表示参数的变化量，在Adagrad中

\[\Delta \theta_t = - \frac{\eta}{\sqrt{G_t + \epsilon}} g_t\]

现在用 $E_t$ 代替 $G_t$ 有

\[\Delta \theta_t = - \frac{\eta}{\sqrt{E_t + \epsilon}} g_t\]

由于分母是梯度的均方根误差，将其简记为 $RMS$ 有

\[\Delta \theta_t = - \frac{\eta}{RMS[g]_t} g_t\]

再定义指数衰减均值

\[E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1 - \gamma) \Delta \theta_t^2\] \[RMS[\Delta \theta]_t = \sqrt{E[\Delta \theta^2]_t + \epsilon}\]

使用 $RMS[\Delta \theta]_{t-1}$ 代替 $\eta$，则得到Adadelta的更新规则

\[\Delta \theta_t = -\frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_t} g_t\] \[\theta_{t+1} = \theta_t + \Delta \theta_t\]

RMSprop

RMSprop的思想和Adadelta类似

\[E_{t+1} = \gamma E_t + (1 - \gamma) g_t^2\] \[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E_t + \epsilon}} g_t\]

Adam

Adam(Adaptive Moment Estimation) 是另一种自适应学习速率的优化算法，它在Adadelta和RMSprop的基础上增加了一个新的类似动量的项

\[m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\] \[v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2\]

$m_t$ 和 $v_t$ 分别是梯度的一阶动量和二阶动量，初值 $m_0 = 0, v_0 = 0$。注意到，在初始阶段，$m_t$ 和 $v_t$ 有一个向初值的偏移，因此，可对一阶动量和二阶动量做偏置校正(bias correction)

\(\hat{m}_t = \frac{m_{t-1}}{1 - \beta_1^t}\) \(\hat{v}_t = \frac{v_{t-1}}{1 - \beta_2^t}\)

然后再更新

\[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t\]

AdaMax

AdaMax在计算 $v_t$ 时使用 $L_p$ 范数代替 $L_2$ 范数

\[v_t = \beta_2^p v_{t-1} + (1 - \beta_2^p) |g_t|^p\]

当 $p$ 变大时，$L_p$ 范数在数值上通常是不稳定的，这也是 $L_1$ 和 $L_2$ 使用得比较多的原因。但是当 $p \rightarrow \infty$ 时，$L_\infty$ 范数又表现出稳定性。为了避免混淆，我们使用 $u_t$ 代替 $v_t$

\[\begin{aligned} u_t & = \beta_2^\infty v_{t-1} + (1 - \beta_2^\infty) |g_t|^\infty \\ & = max(\beta_2 v_{t-1}, |g_t|) \end{aligned}\]

然后使用 $u_t$ 代替 $\sqrt{\hat{v}_t} + \epsilon$ 得到

\[\theta_{t+1} = \theta_t - \frac{\eta}{u_t} \hat{m}_t\]

由于 $u_t$ 的计算依赖于 $max$ 操作，$m_t$ 和 $v_t$ 不再偏移向0点，因此这里不再做偏移校正。通常取 $\eta = 0.001, \beta_1 = 0.9, \beta_2 = 0.999$。

Nadam

Nadam(Nesterov-accelerated Adaptive Moment Estimation)在Adam的基础上融合了NAG的理念，把Adam的更新公式中的 $\hat{m}_t$展开得到

\[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\frac{\beta_1 m_{t-1}}{1 - \beta_1^t} + \frac{(1 - \beta_1) g_t}{1 - \beta_1^t})\]

注意到 $\frac{\beta_1 m_{t-1}}{1 - \beta_1^t}$ 是前一时刻动量项的偏置校正估计，因此可以把它替换为 $\hat{m}_{t-1}$

\[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\beta_1 \hat{m}_{t-1} + \frac{(1 - \beta_1) g_t}{1 - \beta_1^t})\]

然后借签NAG的思想，把 $t-1$ 时刻的动量替换为 $t$ 时刻的动量，这就是Nadam的更新规则

\[\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} (\beta_1 \hat{m}_t + \frac{(1 - \beta_1) g_t}{1 - \beta_1^t})\]

SGD小结

上图展示了一些优化算法在损失平面等高线上的行为，我们可以看到，Adagrad, Adadelta, RMSprop 可以快速右转并收敛；而NAG和Momentum会跑偏。NAG因为“往前看”会比Momentum更快地纠正方向。

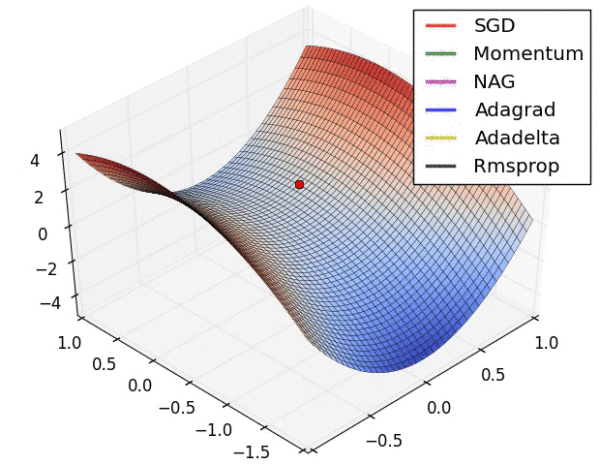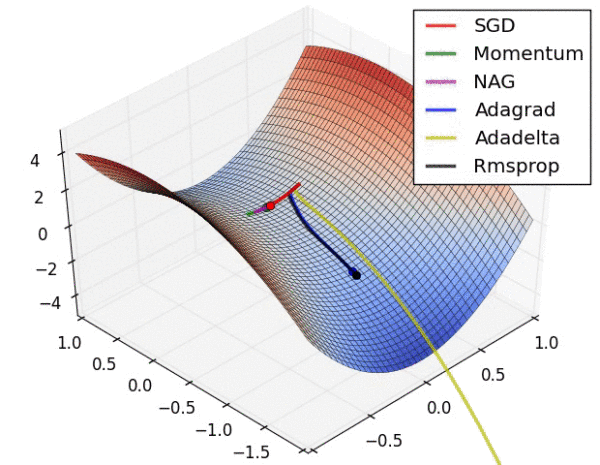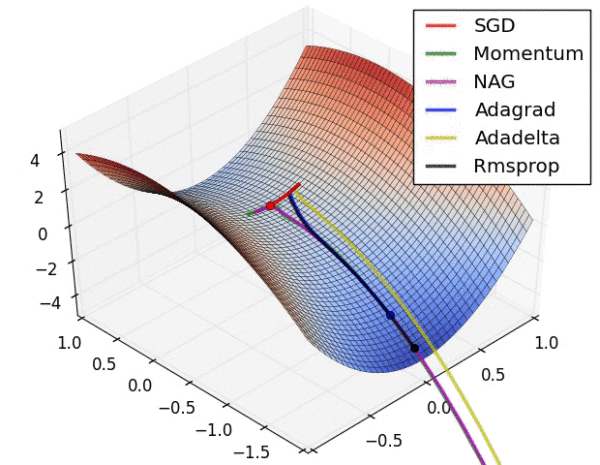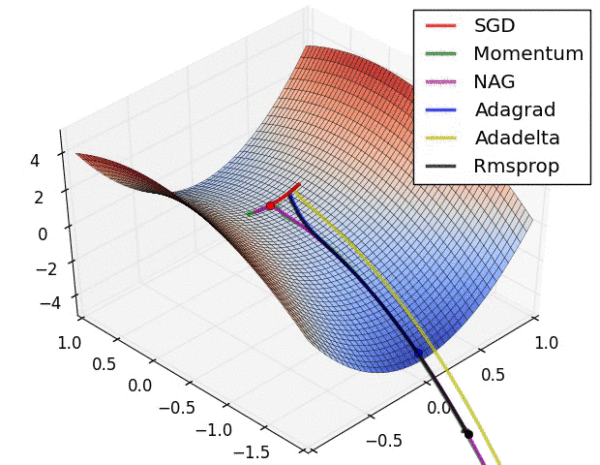
上图展示了优化算法在鞍点处的行为，可以看到，SGD, Momentum和NAG在鞍点处都遇到了困难，反复震荡，尽管Momentum和NAG最终都逃离了鞍点。而Adagrad, Adadelta和RMSprop会快速找到下降的方向，其中Adadelta下降的最快。

牛顿法

根据泰勒公式，若函数 $f(x)$ 在 $x_0$ 处n阶可导，则 $f(x)$ 可以在 $x_0$ 处展开为下式

\[f(x) = \frac{f(x_0)}{0!} + \frac{f'(x_0)}{1!}(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + \dots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x)\]

如果我们忽略2次以上的项，得到

\[f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{1}{2}f''(x_0)(x-x_0)^2\]

如果我们要找极值，就令上式导数为0，即

\[f'(x) = f'(x_0) + f''(x_0)(x-x_0) = 0\]

得到

\[x = x_0 - \frac{f'(x_0)}{f''(x_0)}\]

这就是牛顿法的更新公式，给定 $x_0$，使用上面的公式进行迭代，直到达到一定的精度或者达到最大迭代次数。上面介绍的是一元函数，对于多元函数，二阶泰勒展开可推广为

\[f({\bf{x}}) = f({\bf{x}}_0) + \nabla f({\bf{x}}_0)({\bf{x}}-{\bf{x}}_0) + \frac{1}{2} ({\bf{x}}-{\bf{x}}_0)^T \nabla^2 f({\bf{x}}_0) ({\bf{x}}-{\bf{x}}_0)\]

其中，$\nabla f$ 为 $f({\bf{x}})$ 的梯度向量，$\nabla^2 f({\bf{x}})$ 为 $f({\bf{x}})$ 的Hessian矩阵，其定义分别为

\[\nabla f = \left[ \begin{matrix} {\partial f \over \partial x_1} \\ {\partial f \over \partial x_2} \\ \vdots \\ {\partial f \over \partial x_n} \\ \end{matrix} \right]\] \[\nabla^2 f = \left[ \begin{matrix} {\partial^2 f \over \partial x^2_1} & {\partial^2 f \over \partial x_1 x_2} & \cdots & {\partial^2 f \over \partial x_1 x_n} \\ {\partial^2 f \over \partial x_2 x_1} & {\partial^2 f \over \partial x^2_2} & \cdots & {\partial^2 f \over \partial x_2 x_n} \\ \vdots & \vdots & \ddots & \vdots \\ {\partial^2 f \over \partial x_n x_1} & {\partial^2 f \over \partial x_n x_2} & \cdots & {\partial^2 f \over \partial x^2_n} \\ \end{matrix} \right]\]

分别用 $g$ 和 $H$ 表示 $\nabla f$ 和 $\nabla^2 f$，则得到更新公式

\[{\bf{x}} = {\bf{x}}_0 - H^{-1}__0} g__0}\]

上图是牛顿法和SGD收敛速度的对照，红线是牛顿法，绿线是SGD，可以看出牛顿法的收敛速度比SGD更快。

拟牛顿法

牛顿法虽然收敛比较快，但它需要计算Hessian矩阵及其逆矩阵，会大大增加计算量；同时Hessian矩阵无法保持正定，即无法求逆。为了克服这两个缺点，人们提出了拟牛顿法，其主要思想是，构造出可以近似Hessian矩阵的正定对称矩阵，在这个条件下优化目标函数。常用的拟牛顿算法有DFP、BFGS、L-BFGS。

参考

[1]An overview of gradient descent optimization algorithms