随机模拟也叫蒙特卡罗模拟(Monte Carlo Simulation)，其中一个重要的问题就是，给定一个概率分布p(x),如何在计算机中生成它的样本。通常来讲，生成均匀分布 $Uniform(0,1)$ 的样本是相对容易的，使用线性同余发生器就可以生成伪随机数

\[x_{n+1} = (a x_n + b) \mod m\]

这样生成的伪随机序列与均匀分布的理论计算结果非常接近，可以当成真实的随机数使用。

Box-Muller 变换

如果随机变量 $U_1$, $U_2$ 独立且 $U_1, U_2 \sim Uniform(0,1)$

\[Z_0 = \sqrt{-2 \ln U_1}\cos(2\pi U_2)\] \[Z_1 = \sqrt{-2 \ln U_1}\sin(2\pi U_2)\]

则 $Z_0, Z_1$ 相互独立且服从正态分布。其它一些常见的连续分布，如t分布，F分布，Beta分布，Gamma分布等，都可以通过类似的方式从均匀分布转化得到。但是如果概率分布函数比较复杂，无法通过这些常见的分布变换，那么该如何采样呢？

接受-拒绝采样(Acceptance-Rejection Sampling)

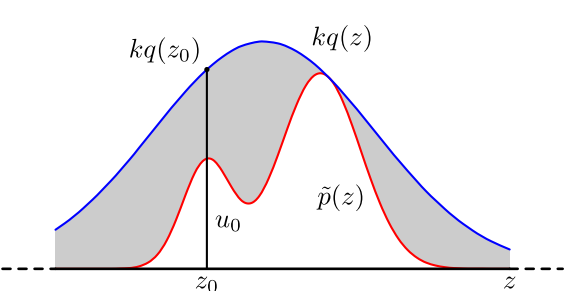
如上图所示，$p(x)$ 是一个很复杂的概率密度函数，为了对其采样，我们可以设定一个可抽样的分布 $q(x)$ (也叫 proposal distribution)，以及常量 $k$，使得 $p(x)$ 总是落在 $kq(x)$ 的下方，即 $p(x) \leq kq(x)$, 接下来重复以下步骤采样：

1. 从 $q(x)$ 中抽样得到 $a$
2. 从均匀分布 $U(0, kq(a))$ 中抽样得到 $u$
3. 若点 $(a, u)$ 落在上图灰色区域，即 $u > p(a)$ 则拒绝本次抽样，否则接受

接受-拒绝采样有两个问题，一是在高维情况下难以找到合适的 $q$ 分布；另一个是不恰当的 $k$ 值会使得第3步中的拒绝率很高，无用计算增加。

MCMC(Markov Chain Monte Carlo)方法

马氏链定理

简单回顾一下HMM这篇文章介绍的马尔科夫链，在马尔科夫链中，任意时刻的状态只与前一个状态有关，用数学公式表示为

\[P(x_{t+1}=x \vert x_t, x_t-1, ..., x_0) = P(x_{t+1}=x \vert x_t)\]

马氏链定理： 如果一个非周期马氏链具有状态转移概率矩阵 $P$, 且它的任何两个状态是连通的，那么 $\lim_{n \to \infty} P_{ij}^n$ 存在且与 $i$ 无关，记为 $\lim_{n \to \infty} P_{ij}^n = \pi(j)$, 有

1. \[\lim_{n \to \infty} P^n = \begin{bmatrix} \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \end{bmatrix}\]
2. $\pi(j) = \sum_{i=0}^{\infty} \pi(i) P_{ij}$
3. $\pi$ 是方程 $\pi P = \pi$ 的唯一非负解，其中 \(\pi = [\pi(1), \pi(2), \cdots, \pi(j), \cdots], \ \ \ \ \sum_i \pi(i) = 1\)

$\pi$ 称为马氏链的平稳分布。马氏链的这一收敛行为非常重要，它是所有MCMC方法的理论基础。设想有一个概率密度函数 $p(x)$，如果我们能构造一个转移矩阵为 $P$ 的马氏链，使得该马氏链的平稳分布刚好是 $p(x)$, 那么我们从任意一个初始状态 $x_0$ 出发，沿着马氏链转移，得到一个序列 $\lbrace x_1, x_2, \cdots, x_n, x_{n+1}, \cdots \rbrace$, 如果马氏链在第n步时已经收敛，那么 $\lbrace x_n, x_{n+1}, \cdots \rbrace$ 就是 $p(x)$ 的样本。如何构造转移矩阵呢？细致平稳条件定理为我们提供了理论基础：

细致平稳条件： 如果非周期马氏链的转移矩阵 $P$ 和分布 $\pi(x)$ 满足

\[\pi(i)P_{ij} = \pi(j)P_{ji}, \ \ \ \ for \ all \ i,j\]

则 $\pi(x)$ 是马氏链的平稳分布，上式被称为平稳细致条件(detailed balance condition)。该定理的证明是比较容易的

\[\sum_i \pi(i)P_{ij} = \sum_i \pi(j)P_{ji} = \pi(j) \sum_i P_{ji} = \pi(j)\] \[\Rightarrow \pi P = \pi\]

因此 $\pi$ 是平稳分布。

MCMC采样

假设我们有一个转移矩阵为 $Q$ 的马氏链，$q(i,j)$ 表示状态从 $i$ 转移 $j$ 的概率。显然通常情况下

\[p(i)q(i,j) \neq p(j)q(j,i)\]

也就是细致平稳条件不成立。为了使上式左右两边相等，我们可以对马氏链做一个改造，在两边各引入一个新的项 $\alpha$, 其中

\[\alpha(i,j) = p(j)q(j,i), \alpha(j,i) = p(i)q(i,j)\]

则有

\[p(i) \underbrace{ q(i,j)\alpha(i,j)}_{q\prime(i,j)} = p(j) \underbrace{q(j,i)\alpha(j,i)}_{q\prime(j,i)}\]

于是，我们把一个具有转移矩阵 $Q$ 的马氏链改造成了一个具有转移矩阵 $Q\prime$ 的马氏链，且 $Q\prime$ 满足细致平稳条件，其平稳分布就是 $p(x)$。上述过程中引入的 $\alpha(i,j)$ 称为接受率，可以理解为原马氏链从状态 $i$ 以 $p(i,j)$ 的概率转移到状态 $j$ 时，以 $\alpha(i,j)$ 的概率接受这个转移。MCMC采样方法总结如下：

1. 初如化马氏链初始状态为 $x_0$
2. 对 $t = 1, 2, …$
   • 第 $t$ 个时刻状态为 $x_t$, 采样 $y \sim p(x \vert x_t)$
   • 从均匀分布采样 $u \sim U(0,1)$
   • 如果 $u < \alpha(x_t, y) = p(y)q(x_t \vert y)$，则接受转移，$x_{t+1} = y$；否则拒绝，$x_{t+1} = x_t$

由于接受率 $\alpha(i,j)$ 可能偏小，导致采样过程中拒绝率较高，收敛到平稳分布的速度较慢。为了提高接受率，我们可以适当放大 $\alpha(i,j)$ 的值，令

\[\alpha(i,j) = \min \lbrace \frac{p(j)q(j,i)}{p(i)q(i,j)}, 1 \rbrace\]

这就是 Metropolis-Hastings 采样算法，简称M-H采样。

Gibbs采样

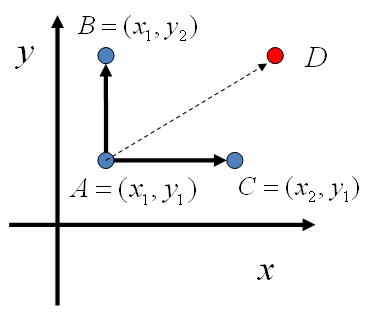
对于高维情形，由于 $\alpha$ 通常小于1, 上述M-H算法仍然不够高效。能不能找到一个转移矩阵 $Q$, 使得 $\alpha = 1$ 呢？我们先看二维的情形，假设有一个概率分布 $p(x,y)$, 考察 $x$ 坐标相同的两个点 $A(x_1, y_1)$ 和 $B(x_1, y_2)$

\(p(x_1,y_1)p(y_2 \vert x_1) = p(x_1)p(y_1 \vert x_1)p(y_2 \vert x_1)\) \(p(x_1,y_2)p(y_1 \vert x_1) = p(x_1)p(y_2 \vert x_1)p(y_1 \vert x_1)\)

从而得到

\[p(A)p(y_2 \vert x_1) = p(B)p(y_1 \vert x_1)\]

上述等式告诉我们，在 $x=x_1$ 这条平行于y轴的直线上，如果使用条件分布 $p(y \vert x_1)$ 作为两个点之间的转移概率，那么任意两点之间的满足细致平稳条件。在 $y=y_1$ 这条直线上我们可以得到一样的结论。于是我们可以构造平面上两点之间的转移概率矩阵 $Q$

\[\begin{cases} & Q(A,B) = p(y_B \vert x_A), \ \ \ \ if \ x_A = x_B \\ & Q(A,C) = p(x_C \vert y_A), \ \ \ \ if \ y_A = y_C \\ & Q(A,D) = 0, \ \ \ \ others \end{cases}\]

我们很容易证明，平面上任意两点 $A, B$, 满足细致平稳条件

\[p(A)Q(A,B) = p(B)Q(B,A)\]

这就是 Gibbs 采样算法。其过程总结如下：

1. 随机初始化 $(x_0, y_0)$
2. 对 $t=1,2,…$
   • $y_{t+1} \sim p(y \vert x_t)$
   • $x_{t+1} \sim p(x \vert y_{t+1})$

参考

[1]. https://www.cnblogs.com/xbinworld/p/4266146.html
[2]. http://www.cnblogs.com/pinard/p/6625739.html
[3]. https://blog.csdn.net/zongzi13545329/article/details/63685816